Q1: Sam has 3x + 4 dollars saved. Tessa has saved 7x + 16 dollars. Together they
have $110 saved. How much money have they each saved individually?
Answers
Answer:
450
Step-by-step explanation:
Related Questions
In ΔRST, the measure of ∠T=90°, the measure of ∠R=67°, and TR = 94 feet. Find the length of RS to the nearest tenth of a foot.

Answers
Answer:
the length of RS to the nearest tenth of a foot is 240.6ft

4x+3y=9 and 3x +4y = 36
Answers
The solution of the system of equations:
( -16.7, 19.28)
How to solve the system of equations?
Here we have the system:
4x+3y=9
3x +4y = 36
First, we need to isolate one of the variables in one of the equations, let's isolate x on the second one:
x = 36/3 - (4/3)y = 9 - (4/3)y
Now we can replace this in the other equation:
4*(9 - (4/3)y) + 3y = 9
36 - (16/3)y + (9/3)y = 9
- (7/3)y = -36 - 9 = -45
y = (3/7)*45 = 19.28
To get the value of x, we get:
x = 9 - (4/3)*19.28 = -16.7
Then the solution of the system is ( -16.7, 19.28)
If you want to learn about systems of equations:
https://brainly.com/question/13729904
#SPJ1
A hospital tracked the day of the week each baby was born and whether or not the delivery was scheduled in advance. The following two-way table displays data for the sample of babies born in a particular year at that hospital. Day of birth Scheduled Unscheduled TOTAL
Sunday 999 313131 404040
Monday 191919 666666 858585
Tuesday 202020 707070 909090
Wednesday 171717 616161 787878
Thursday 191919 686868 878787
Friday 151515 555555 707070
Saturday 111111 393939 505050
TOTAL 110110110 390390390 500500500
Find the probability that a randomly selected baby from this sample was born on Tuesday OR on Friday
Answers
There is a very small chance (less than 1%) that a randomly selected baby from this sample was born on Tuesday OR on Friday.
To find the probability that a randomly selected baby from this sample was born on Tuesday OR on Friday, we need to add the number of babies born on Tuesday to the number of babies born on Friday, and then divide by the total number of babies in the sample.
The number of babies born on Tuesday is 202020, and the number of babies born on Friday is 151515. Therefore, the total number of babies born on Tuesday or on Friday is 202020 + 151515 = 353535.
The total number of babies in the sample is 500500500. Therefore, the probability that a randomly selected baby from this sample was born on Tuesday OR on Friday is:
353535 / 500500500 = 0.0007061
It is interesting to note that the number of babies born on different days of the week varies in this sample. For example, there are more babies born on weekdays (Monday-Friday) than on weekends (Saturday and Sunday), and there are more babies born on Tuesday than on Wednesday or Thursday.
The number of scheduled deliveries is higher than the number of unscheduled deliveries overall, but there are some days (e.g., Friday and Saturday) where there are more unscheduled deliveries than scheduled deliveries. These patterns could be explored further to understand the factors that influence the timing and scheduling of deliveries.
Learn more about probability here:
https://brainly.com/question/14210034
#SPJ4
CAN I GET SOME HELP PLEASE?

Answers
Answer:
m = 8
n = 9
Step-by-step explanation:
Remark
By similar triangles
(m - 4) /8 = 8 / 2m Cross multiply
2m(m - 4) = 64 Expand the left
2m^2 - 8m = 64 Divide through by 2
m^2 - 4m = 32 Subtract 32 from both sides.
m^2 - 4m - 32 = 0 Factor
(m - 8)(m + 4) = 0
m + 4 has no meaning in geometry. - numbers cannot be distances.
m - 8 = 0
m = 8
===================
By the same kind of similar triangles used in problem A we get
7 / x = x / 9
x^2 = 63
Just leave this as it is. We'll solve this by the Pythagorean Theorem.
x^2 + 9^2 = (n + 3)^2
63 + 81 = (n + 3)^2
144 = (n + 3)^2 Take the square root of both sides
12 = n + 3 Subtract 3 from both sides.
9 = n
How does changing the sign of the constant a from positive to negative affect the domain and range of f(x) = a|x|?
Answers
When changing the sign of the constant a from positive to negative, the domain remains the same. But the range changes.
A function's range is the set of all values it can accept, whereas its domain is the set of all values for which it is defined.
Consider the given function f(x)=a|x|. Let us consider "a" takes positive values that is \(a\geq0\). Then, the given function is defined as follows,
\(f(x)=\begin{cases}a(x)=ax}\; &x\geq0\\{a(-x)=-ax\;&x < 0\end{cases}\)
Then, the domain will be \(\text{domain}=\mathbb{R}\{(-\infty, \infty)\) and the range will be given as \(\text{Range} = \text{only non-negative real numbers} = \mathbb{R}^++\{0\}\).
Now let us consider "a" takes negative values that is a<0. Then, the given function is defined the same and the domain will remain the same. But the range will be given as \(\text{Range} = \text{only negative real numbers} = \mathbb{R}^-+\{0\}\).
To know more about domain and range:
https://brainly.com/question/29452843
#SPJ4
Kelly spends 5 hours each week playing softball and 4 hours each week practicing her violin. Write the ratio of hours spent practicing violin to hours spent playing softball three different ways.
Answers
Given:
Kelly spends 5 hours each week playing softball and 4 hours each week practicing her violin.
To find:
The ratio of hours spent practicing violin to hours spent playing softball three different ways.
Solution:
We have,
Time spend on Softball = 5 hours
Time spend on Violin = 4 hours
The ratio to hours spent practicing violin to hours spent playing softball is
\(\text{Required ratio}=\dfrac{\text{Time spend on Violin}}{\text{Time spend on Softball}}\)
\(\text{Required ratio}=\dfrac{4}{5}\)
It can be written as
\(\text{Required ratio}=4:5\)
\(\text{Required ratio}=4\text{ to }5\)
Therefore, the ratio of hours spent practicing violin to hours spent playing softball three different ways are \(\dfrac{4}{5}, 4:5\) and 4 to 5.
Given f(x)=3x-1, solve for x when f(x)=-7.

Answers
Answer:
x = -2
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Algebra I
Function NotationStep-by-step explanation:
Step 1: Define
f(x) = 3x - 1
f(x) = -7
Step 2: Solve for x
Substitute: -7 = 3x - 1Isolate x term: -6 = 3xIsolate x: -2 = xRewrite: x = -2The area of a sector is 30 m2 in a circle with radius 4 m. What is the arc length of the sector?
Answers
Answer:
15 m
Step-by-step explanation:
The area of the circle is
A =pi r^2
A = pi 4^2 = 16 pi
The area of the sector is 30
The fraction is
30/16 pi
Take this time 2pi which are the radians of a circle
30 /16 pi * 2 pi = 15/4
This is the number of radians the angle is
The arc length is s = r * theta where theta is in radians
s = r theta
= 4 * 15/4
= 15
i need help with dis

Answers
Answer:
A. (0, 1)
B. (10, 4)
C. (7, 7)
D. (5, 10)
Step-by-step explanation:
When changing coordinates over the y-axis, use the formula (x, y) = (-x, y)
The recipe uses 1/2 cup of sugar for 1 cup of flour...how much flour should there be if there is 2 cups of sugar? *
Answers
Answer:
4 cups
Step-by-step explanation:
2 divided by 1/2 is 4 so there are 4 half cups of sugar.
Since the sugar is multiplied by 4 you have to multiply the flour by 4.
1*4=4
In a random sample of 200 items, 5 items were defective. An estimate of the percentage of defective items in the population is.
Answers
If 5 out of 200 things were flawed, the population's estimated defect percent would be 2.5%.
What is percentage?Percent, which is a relative figure used to denote hundredths of any amount. Since one percent (symbolized as 1%) is equal to one tenth of anything, 100 percent stands for everything, while 200 percent refers to double the amount specified. The word "percent" simply refers to "per hundred," and the sign for percentage is %. By multiplying the total or whole number by 100, one percent (or 1%) is equal to one hundredth of the whole or whole.
Here,
Total number of items=200
number of defective items=5
Percentage of defective items,
=5/200*100
=2.5%
Therefore, if 5 out of 200 things were defective, the population's estimated percentage of defective items is 2.5%.
To know more about percentage,
https://brainly.com/question/27819277
#SPJ4
Use the table to write a linear function that relates y to x.

Answers
y=-1x/4
this is the best way to represent this,
A recipe for a pitcher of lemonade calls for 7/8 cup of sugar, 3/4 cup of lemon juice, and 3 3/4 cups of water. How many total cups of sugar, lemon juice, and water will be needed for three pitchers of
lemonade?
Answers
Answer:
12 tablespoons of sugar and 3 cups of water (48 tablespoons)
Step-by-step explanation:
Hope helps you
<3
ANSWER PROPERLY FOR BRAINLIEST OR ELSE I REPORT

Answers
Answer:
A: 0.3
B: 0.3
Step-by-step explanation:
Basically both answers are the same
2. Please help me out!!

Answers
Answer:
x = 6Step-by-step explanation:
JKM + MKL = JKL
9x - 10 + 83 = 127
9x = 127 - 83 + 10
x = 54 / 9
x = 6
Please help me :(.......

Answers
Answer:
He makes £470 profit
Step-by-step explanation:
He pays $160 for 60 jumpers.
He sells 80% (48) for $12 each. Income of $576
He puts the remaining (12) on sale for one full one half off.
He sells 3 for half price ($6) and 3 for full price ($12) Income of $54
$576 + $54 = $630
$630 - $160 = $470
In pounds sorry about the USD
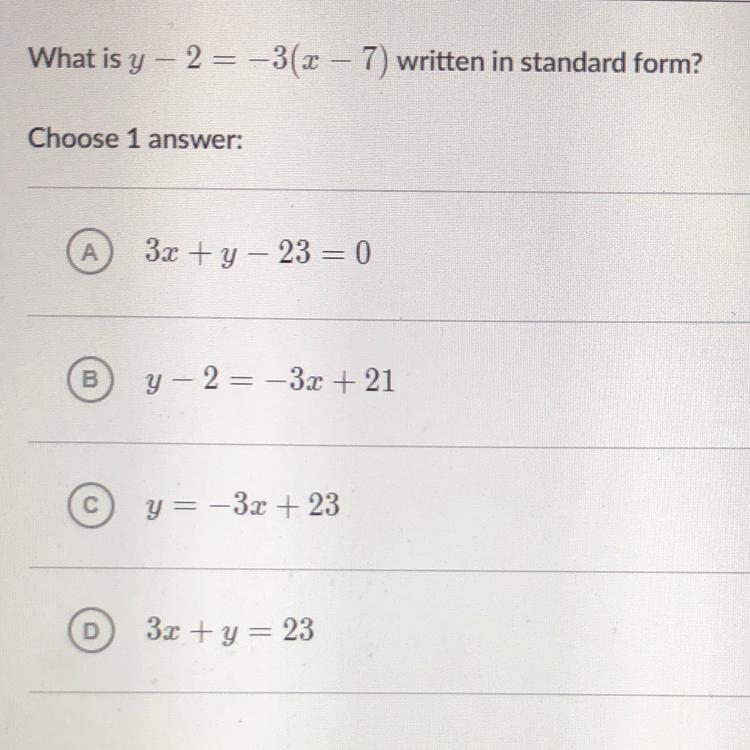
what is y- 10 = 9(x + 8) in standard form
Answers
“9x-y= -82”
Hope this helps:)
A teacher has an annual income of $40,400. The income tax the teacher has to pay is 6.5%. What is the amount of income tax the teacher has to pay?
Answers
They will pay $2,626.00 in income taxes.
Find the midpoint of a line segment with endpoints at (-5,7) and (13, 13).
M =(x, y) = 1; + x, y + y;
2. 2?
Answers
Answer:
About 7
Step-by-step explanation:
a researcher obtain a statistically significant r=-.91 when n=30. how would you report this?
Answers
A statistically significant negative correlation coefficient of r = -0.91 was obtained from a sample of n = 30. This indicates a strong and significant negative relationship between the variables.
The researcher conducted a correlation analysis and found a correlation coefficient (r) of -0.91, which indicates a strong negative relationship between the variables under investigation. The negative sign indicates that as one variable increases, the other variable tends to decrease, and vice versa.
The statistical significance of the correlation coefficient is crucial in determining whether the observed relationship is likely to be due to chance or if it truly exists in the population. In this case, the report should highlight that the obtained correlation coefficient is statistically significant.
To establish statistical significance, the researcher likely conducted a hypothesis test, such as a t-test or a permutation test, to determine the probability of obtaining a correlation coefficient as extreme as -0.91 under the null hypothesis of no correlation. Since the obtained correlation coefficient is statistically significant, it suggests that the observed negative relationship is unlikely to be a result of chance and provides evidence for a genuine association between the variables in the population from which the sample was drawn.
Reporting this finding is important for conveying the strength and significance of the negative relationship to the readers, providing valuable insights for further analysis and interpretation of the variables under investigation.
Learn more about correlation coefficient here:
https://brainly.com/question/29704223
#SPJ11
For a certain population of penguins, the distribution of weight is approximately normal with mean 15. 1 kilograms (kg ) and standard deviation 2. 2 kg. Approximately what percent of the penguins from the population have a weight between 13. 0 kg and 16. 5 kg ?.
Answers
56.78% of the penguins in the population have a weight between 13.0 kg and 16.5 kg, according to the usual distribution.
Given,
The mean of the population, μ = 15.1 kg
Standard deviation, σ = 2.2 kg
We have to find the percent of the penguins from the population have a weight between 13. 0 kg and 16. 5 kg;
Here,
z score = x - μ / σ
The z-score calculates how far the measure deviates from the mean by standard deviation.The p-value for this z-score, which is the percentile of X, can be obtained by looking at the z-score table.The ratio of the p-value of Z when X = 16.5 minus the p-value of Z when X = 13 indicates the percentage of penguins in the population whose weight is between 13.0 kg and 16.5 kg.
x = 16.5
z score = x - μ / σ
z = (16.5 - 15.1) / 2.2 = 0.64
Z = 0.64 has a p-value of 0.7389.
x = 13
z score = x - μ / σ
z = (13 - 15.1) / 2.2 = -0.95
Z = -0.95 has a p-value of 0.1711.
0.7389 - 0.1711 = 0.5678.
0.5678 = 56.78% of the penguins from the population have a weight between 13.0 kg and 16.5 kg.
Learn more about population here;
https://brainly.com/question/27556504
#SPJ4
If \( P(B)=0.2, P(A \mid B)=0.9, P\left(B^{\prime}\right)=0.8 \), and \( P\left(A \mid B^{\prime}\right)=0.5 \), find \( P(B \mid A) \). \( P(B \mid A)= \) (Round to three decimal places as needed.)
Answers
P(B∣A) is approximately 0.310, rounded to three decimal places.
To find the probability P(B∣A), we can use Bayes' theorem:
P(B∣A)= P(A) / P(A∣B)⋅P(B)
Given information:
P(B)=0.2
P(A∣B)=0.9
P(B')=0.8 (probability of not B)
P(A∣B′)=0.5 (probability of A given not B)
First, we need to calculate
P(A), the probability of event A. We can use the law of total probability to express P(A) in terms of the probabilities related to B and not B:
P(A)=P(A∣B)⋅P(B)+P(A∣B′)⋅P(B′)
Substituting the given values:
P(A)=0.9⋅0.2+0.5⋅0.8=0.18+0.4=0.58
Now, we can substitute the known values into Bayes' theorem:
P(B∣A)= P(A)/ P(A∣B)⋅P(B)
= 0. 9.0.2 / 0.58
Calculating this expression:
P(B∣A)≈ 0.5 80.18 ≈0.310
Therefore, P(B∣A) is approximately 0.310, rounded to three decimal places.
for such more question on probability
https://brainly.com/question/13604758
#SPJ8
How many ways can 4 people sit in a table of 6 seats? A.120
B.24
C.360
D.15
Answers
Answer:
I thought it would be 24
The area enclosed by a circular fountain is 78.57 m². What is the diameter of the
fountain? Round your answer to the nearest meter.
Answers
Answer:
multiply the radius by 2 to get the diameter.
Step-by-step explanation:
When planting a garden, you can choose from five types of tomatoes, two types of peppers, and four types of squash. If you choose only one crop from each category, how many possible garden combinations can you make?
When building a computer, you need to make several choices, such as type of storage, level of memory, and type of processor. You can choose from three types of storage, six levels of storage, and four types of processor. Calculate the number of combinations that you have if these are the only three choices you need to make.
Answers
There are 72 possible combinations for the computer choices.For the garden combinations, since you are choosing one crop from each category, you can use the concept of multiplication to determine the total number of combinations.
Number of tomato choices = 5
Number of pepper choices = 2
Number of squash choices = 4
Total number of garden combinations = Number of tomato choices * Number of pepper choices * Number of squash choices
Total number of garden combinations = 5 * 2 * 4 = 40
Therefore, there are 40 possible garden combinations you can make.
For the computer combinations, using the same concept of multiplication:
Number of storage choices = 3
Number of memory level choices = 6
Number of processor choices = 4
Total number of computer combinations = Number of storage choices * Number of memory level choices * Number of processor choices
Total number of computer combinations = 3 * 6 * 4 = 72
Therefore, there are 72 possible combinations for the computer choices.
To learn more about Multiplication click here:
brainly.com/question/12507051
#SPJ11
Solve for a.
ab+c=d
a =
b
(c-d)
Oa- (d-c)
b
oa=b+ с

Answers
Answer:
The answer is is the middle answer! a= (d - c)
--------------
b
Step-by-step explanation:
Hope this is helpful! Good Bless youu..
complex numbers are represented on a cartesian coordinate system with a horizontal real axis and a vertical ___ axis.
Answers
Complex numbers are represented on a cartesian coordinate system with a horizontal real axis and a vertical imaginary axis.
Any number that can be expressed as a+bi, where i is the imaginary unit and a and b are the real numbers, is a complex number. The number is made up of two parts: real part (a) and imaginary part (b).
Just like we can use the number line to visualize a set of real numbers, we can use the complex plane to visualize a set of complex numbers. The complex plane consists of two number lines intersecting at a right angle at the point (0,0)(0,0)left parenthesis, 0, comma, 0, right parenthesis.
The horizontal number line (what we know as the xxx-axis on a Cartesian plane) is the real axis. The imaginary axis is the vertical number line (the yyy-axis on a Cartesian plane).A point in the complex plane can represent every complex number.
For example, consider the number 3-5i3−5i3, minus 5, i. This number, also expressed as 3+(-5)i, has a real part of 3 and imaginary part of -5. The location of this number on the complex plane is the point that corresponds to 3 on the real axis and -5 on the imaginary axis.
So the number 3+(-5) corresponds with the point (3,-5). In the general complex number, a+bi corresponds to the complex plane's point(a,b).
Hence, complex numbers are represented on a cartesian coordinate system with a real horizontal axis and an imaginary vertical axis.
Learn more about Cartesian plane:
https://brainly.com/question/28574364
a carpenter is making doors that are 2058.0 millimeters tall. if the doors are too long they must be trimmed, and if they are too short they cannot be used. a sample of 25 doors is made, and it is found that they have a mean of 2045.0 millimeters with a standard deviation of 20.0 . is there evidence at the 0.1 level that the doors are either too long or too short? assume the population distribution is approximately normal. is there sufficient evidence to support the claim that the doors are either too long or too short?
Answers
In the result of hypothesis testing, p-value < 0.1, so null hypothesis can't be rejected. Therefore, there is no evidence to support the claim that doors are either too long or too short.
We have, a carpenter is making doors, The height of door = 2058.0 millimeters. Consider a sample of doors with sample size, n = 25
Sample mean, μ = 2045 mili meters
Standard deviations, σ = 20
Level of significance, α = 0.1 for either too long or too short. Here, we considered population distribution is approximately normal. Using the hypothesis testing for support the claim, the null and alternative hypothesis are defined as
\(H_o: \mu = 2058\)
\(H_a: \mu ≠ 2058\)
Now, we z-test to determine test statistic value,
\(Z =\frac{ X - \mu}{\sigma}\)
Substitute all known values in above formula,
\(=\frac{ 2045 - 2058}{20}\)
= - 0.65
Using the normal distribution table the value of P value for z = - 0.65 is equals to 0.257846. So, p-value =0. 257846> 0.01.
Hence, the claim is not true.
For more information about hypothesis testing, refer:
https://brainly.com/question/15980493
#SPJ4
I need help pls so I can get a good grade
Answers
Answer:
Step-by-step explanation:
C is the answer.
Adrian bought a car worth $12000 on 36 easy installments of $375. Answer the following questions. (1) How much total amount did Adrian pay in 36 months? Answer: Total payment A = $ (2) Identify the letters used in the simple interest formula I = Prt. I= $ P= $ and t years. (3) Find the rate of interest in percentage. Answer: r %. ASK YOUR TEACHER
Answers
3) since we don't have the information about the interest paid (I), we cannot determine the rate of interest at this time.
(1) To find the total amount Adrian paid in 36 months, we can multiply the monthly installment by the number of installments:
Total payment A = Monthly installment * Number of installments
= $375 * 36
= $13,500
Therefore, Adrian paid a total of $13,500 over the course of 36 months.
(2) In the simple interest formula I = Prt, the letters used represent the following variables:
I: Interest (the amount of interest paid)
P: Principal (the initial amount, or in this case, the car worth)
r: Rate of interest (expressed as a decimal)
t: Time (in years)
(3) To find the rate of interest in percentage, we need more information. The simple interest formula can be rearranged to solve for the rate of interest:
r = (I / Pt) * 100
To know more about Number visit:
brainly.com/question/3589540
#SPJ11