Identify the terminal point for a 45° angle in a unit circle.
Answers
9514 1404 393
Answer:
(x, y) = ((√2)/2, (√2)/2))
Step-by-step explanation:
See the attached chart. The 45° angle can be found in the upper-right portion of the chart (1st quadrant).

Related Questions
14) Evaluate each indefinite integral. SHOW STEPS

Answers
As a result, -3/10 csc⁵-3x + C is the antiderivative of 9csc-3xcot-3x⋅ csc³-3x.
What is meant by an integral in math?In mathematics, an integral is either a number representing the region under a function's graph for a certain interval or an added to the initial, the derivative which is the previous function (indefinite integral).
9csc-3xcot-3x ⋅ csc³-3x = 9csc⁴-6x cot-3x
Then, we can use u-substitution, with u = csc-3x and du/dx = -3csc-3xcot-3x dx, as in the previous problem. We get:
∫9csc-3xcot-3x⋅ csc³-3x dx = -3/2 ∫u⁴ du
= -3/2 × u⁵ / 5 + C
= -3/10 csc⁵-3x + C
Therefore, the antiderivative of 9csc-3xcot-3x⋅ csc³-3x is -3/10 csc⁵-3x + C.
To know more about integral visit:
https://brainly.com/question/18125359
#SPJ1
SHARE 300 USING 2:3:5
Answers
If we divide 300 into parts using the ratio 2:3:5, we get:
2 parts = 2/10 of the total ratio = 2/10 x 300 = 60
3 parts = 3/10 of the total ratio = 3/10 x 300 = 90
5 parts = 5/10 of the total ratio = 5/10 x 300 = 150
Therefore, 300 divided in the ratio 2:3:5 would result in three parts of 60, 90, and 150.
I hope I helped!
~~~Harsha~~~
In a bag there are 3 pink, 5 blue, 3 yellow, and 1 purple jellybeans. What is the probability of picking a jellybean that is NOT blue? Is this theoretical or experimental probability? Why?
Answers
!:
If you could mark as brainliest that would be great!
Answer:
The probability of picking a jellybean that is NOT blue is:
(number of jellybeans that are not blue) / (total number of jellybeans)
= (3 + 3 + 1) / (3 + 5 + 3 + 1)
= 7/12
This is theoretical probability because it is based on the assumption that each jellybean has an equal chance of being picked, without actually performing the experiment.
Answer: The probability of picking a jellybean that isn’t blue is has a 7/12 chance. This is a theoretical probability because you never can exactly tell if you’re gonna pick blue or not.
(The underlined parts are your answers.)
Step-by-step explanation: Have a great day <3
Is (6,0) a solution of 5x-y=9?
Answers
Answer:
No
Step-by-step explanation:
5(6)-(0)≠95(6)-(0)=30help please giving branliest

Answers
Answer:
C) 53°
Step-by-step explanation:
We know that <3 and <4 are equal, so we can solve for y.
3y+7=5y-73
7+73=5y-3y
80=2y
y=40
Now plug that in to <3
3y+7=3(40)+7=127
We know that <3 and <2 equal 180.
180-127=53
So <2=53°
I WILL GIVE CROWN
Jim has a bank account balance of −$15.46. As soon as he realizes this, he deposits $25.50 in the account.
What is Jim's bank account balance after the deposit is made?
Enter your answer in the box.
$
Answers
Answer:
the answer would be 773/1275 if your dividing if its multiplying its -394.24
Answer:
I know I'm late to answer this but the its 10.04 I hope this helps :D
Step-by-step explanation:
Brittany asked her classmates: How much time, in minutes, do you spend reading each day? Here are the results: 10, 20, 20, 20, 30, 30, 30, 30, 30, 40, 40, 40, 60, 60, 60 Display the data in a line plot, a histogram, and a box plot. Next to each graph, write down something you notice about the data. Upload your completed plots here.
Answers
The line plot, histogram, and box plot provide different visual representations of the reading time data. By analyzing these plots, we can observe the distribution and characteristics of the data, such as central tendency, spread, and outliers.
Line Plot:
A line plot displays data points on a number line, representing the frequency or count of each value.
In this case, the line plot will show the minutes spent reading on the x-axis and the count of students on the y-axis.
For the given data, the line plot will show 10, 20, 30, 40, and 60 on the x-axis, with the corresponding counts displayed above each value.
Histogram:
A histogram displays data distribution by dividing the range of values into intervals or bins and representing the frequency of values falling into each bin.
The histogram will have the minutes spent reading on the x-axis and the count or frequency of students on the y-axis.
The intervals will be 10-19, 20-29, 30-39, 40-49, and 50-59, with the last interval being 60+.
The height of each bar in the histogram will represent the number of students falling into each interval.
Box Plot:
A box plot (also known as a box-and-whisker plot) provides a visual representation of the distribution of data, including measures of central tendency and variability.
The box plot will show a horizontal line inside a box, with whiskers extending from the box, and possibly individual data points beyond the whiskers.
The box will represent the interquartile range (IQR), showing the middle 50% of the data.
The line within the box will represent the median value.
The whiskers will indicate the minimum and maximum values, excluding outliers.
By analyzing these plots, you can observe the central tendency, spread, and distribution of the reading time data. For example, you can identify any outliers, notice the most common reading durations, and observe any patterns or trends within the dataset.
To learn more about line plot
https://brainly.com/question/16321364
#SPJ8
13. You deposit $5000 each month into an account earning 4.5% interest compounded monthly. (a) How much will you have in the account in 25 years? $ (b) How much total money will you put into the account? $ (c) How much total interest will you earn over the 25 years? $
Answers
Using the future value formula, it is found that:
a) You will have $2,764,990 in the account in 25 years.
b) You will put $1,500,000 into the account in 25 years.
c) You will earn $1,264,990 in interest in 25 years.
What is the future value formula?The future value formula is given as follows:
\(V(n) = P\left[\frac{(1 + r)^n - 1}{r}\right]\)
In which the parameters of the formula are explained as follows:
P is the payment.n is the number of payments.r is the interest rate.Hence the values of these parameters are:
P = 5000, r = 0.045/12 = 0.00375, n = 12 x 25 = 300.
Then the balance of the account after 25 years will be of:
\(V(n) = P\left[\frac{(1 + r)^n - 1}{r}\right]\)
\(V(300) = 5000\left[\frac{(1.00375)^{300} - 1}{0.00375}\right]\)
V(300) = $2,764,990
The amount inserted into the account will be of:
5000 x 25 x 12 = $1,500,000.
Hence the interest earned in 25 years will be of:
2764990 - 1500000 = $1,264,990.
More can be learned about the future value formula at https://brainly.com/question/24703884
#SPJ1
An antique table increases in value according to the function v(x)=550(1.05)x dollars, where x is the number of years after 1990.a. How much was the table worth in 1990?b. If the pattern indicated by the function remains valid, what was the value of the table in 2005?c. Use a table or a graph to estimate the year when this table will reach double its 1990 value

Answers
In 1990 the value of the antique table was:
\(\begin{gathered} v(0)=550(1.05)^0, \\ v(0)=550\cdot1, \\ v(0)=550. \end{gathered}\)In 2005, x=2005-1990=15, therefore:
\(\begin{gathered} v(15)=550(1.05)^{15}\text{.} \\ v(15)\approx1143.41. \end{gathered}\)Graphing the function we get:
Therefore, after approximately 14 years, the antique table will double its value, which corresponds to the year 2004.
Answer:
a) The table was worth $550 in 1990.
b) The value of the table was $1143.41 in 2005.
c) The antique table will double its value in 2004.

Find the value of x round to the nearest tenth

Answers
Answer:
using the SOH CAH TOA
tan●=opp/adj
tan35⁰=12/x
x=12/tan35⁰
x=17.14
PLEASE HELP FAST !!!!!!!!
Identify the equation that represents a quadratic relationship

Answers
Answer:
Step-by-step explanation:
Quadratic means squared equation so
the first one is your answer.
y= 4x²
Help help help help math math

Answers
Answer:
8 i think im not really sure
Step-by-step explanation:
Which equation represents a line that passes through (5, 1) and has a slope of StartFraction one-half EndFraction?
y – 5 = y minus 5 equals StartFraction one-half EndFraction left-parenthesis x minus 1 right-parenthesis.(x –1)
y – y minus StartFraction one-half EndFraction equals 5 left-parenthesis x minus 1 right-parenthesis. = 5(x –1)
y – 1 = y minus 1 equals StartFraction one-half EndFraction left-parenthesis x minus 5 right-parenthesis.(x –5)
y – 1 = 5y minus 1 equals 5 left-parenthesis x minus StartFraction one-half EndFraction right-parenthesis.
Answers
Step-by-step explanation:
Slope 1/2 point 5,1
in point slope form would be
(y-1) = 1/2 (x-5)
why do the hands on the clock form an angle?
Answers
Answer:
The entire clock measures 360 degrees. As the clock is divided into 12 sections. The distance between each number is equivalent to 30 degrees (360/12)
I hope this helps you!
The area of the circular base of a cone is 16π cm², and the slant height of the cone is 4 times the radius of the cone.
What is the approximate lateral area of the cone?
Answers
The approximate lateral area of the cone is equal to 200.96 cm².
How to calculate the lateral area of the cone?Mathematically, the lateral area of a cone can be calculated by using this mathematical expression:
Lateral surface area of a cone, LSA = πrl or πr√(r^2 + h^2)
Where
l represents the slant height of the cone.r represents the radius of the cone.h represents the height of the cone.How to calculate the area of a circle?Mathematically, the area of a circle can be calculated by using this formula:
Area of a circular base = πr²
16π = πr²
Radius, r = √16
Radius, r = 4 cm.
Substituting the given parameters into the lateral area of a cone formula, we have the following;
Lateral surface area of a cone, LSA = πrl = πr4(r)
Lateral surface area of a cone, LSA = 3.14 × 4 × 16
Lateral surface area of a cone, LSA = 200.96 cm².
Read more on surface area here: https://brainly.com/question/27812847
#SPJ1
Answer:
201 beause you are rounding to the nearest whole number
Step-by-step explanation:
100 POINTS
A gazebo in the shape of a regular octagon has equal sides of 9 feet and an apothem of 10.9 feet.
a. If one side of a gazebo is open, and the other sides have a railing, find the cost of the railing if it sells for $7.90 per foot.
b. Find the area of the gazebo in square feet.
c. Find the cost of the gazebo's flooring if it costs $3 per square foot. Round to the nearest hundred dollars.
Answers
Answer:
a) $497.70
b) 392.4 square feet
c) $1,200
Step-by-step explanation:
Part (a)A regular octagon has 8 sides of equal length.
Given each side of the octagon measures 9 feet in length, and one side does not have a railing, the total length of the railing is 7 times the length of one side:
\(\textsf{Total length of railing}=\sf 7 \times 9\; ft=63\;ft\)
If the railing sells for $7.90 per foot, the total cost of the railing can be calculated by multiplying the total length by the cost per foot:
\(\textsf{Total cost of railing}=\sf 63\;ft \times \dfrac{\$7.90}{ft}=\$497.70\)
Therefore, the cost of the railing is $497.70.
\(\hrulefill\)
Part (b)To find the area of the regular octagonal gazebo, given the side length and apothem, we can use the area of a regular polygon formula:
\(\boxed{\begin{minipage}{6cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{n\;s\;a}{2}$\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the length of one side.\\ \phantom{ww}$\bullet$ $a$ is the apothem.\\\end{minipage}}\)
Substitute n = 8, s = 9, and a = 10.9 into the formula and solve for A:
\(\begin{aligned}\textsf{Area of the gazebo}&=\sf \dfrac{8 \times 9\:ft \times10.9\:ft}{2}\\\\&=\sf \dfrac{784.8\;ft^2}{2}\\\\&=\sf 392.4\; \sf ft^2\end{aligned}\)
Therefore, the area of the gazebo is 392.4 square feet.
\(\hrulefill\)
Part (c)To calculate the cost of the gazebo's flooring if it costs $3 square foot, multiply the area of the gazebo found in part (b) by the cost per square foot:
\(\begin{aligned}\textsf{Total cost of flooring}&=\sf 392.4\; ft^2 \times \dfrac{\$3}{ft^2}\\&=\sf \$1177.2\\&=\sf \$1200\; (nearest\;hundred\;dollars)\end{aligned}\)
Therefore, the cost of the gazebo's flooring to the nearest hundred dollars is $1,200.
a. To find the perimeter of the gazebo, we can use the formula P = 8s, where s is the length of one side. Substituting s = 9, we get:
P = 8s = 8(9) = 72 feet
Since one side is open, we only need to find the cost of railing for 7 sides. Multiplying the perimeter by 7, we get:
Cost = 7P($7.90/foot) = 7(72 feet)($7.90/foot) = $4,939.20
Therefore, the cost of the railing is $4,939.20.
b. To find the area of the gazebo, we can use the formula A = (1/2)ap, where a is the apothem and p is the perimeter. Substituting a = 10.9 and p = 72, we get:
A = (1/2)(10.9)(72) = 394.56 square feet
Therefore, the area of the gazebo is 394.56 square feet.
c. To find the cost of the flooring, we need to multiply the area by the cost per square foot. Substituting A = 394.56 and the cost per square foot as $3, we get:
Cost = A($3/square foot) = 394.56($3/square foot) = $1,183.68
Rounding to the nearest hundred dollars, the cost of the flooring is $1,184. Therefore, the cost of the gazebo's flooring is $1,184.
#SPJ1
{3x+y=7{-2x+y=-3 please
Answers
Answer:
x=\(\frac{4}{5}\)
y=\(\frac{23}{5}\)
Step-by-step explanation:
Look at the pictures!
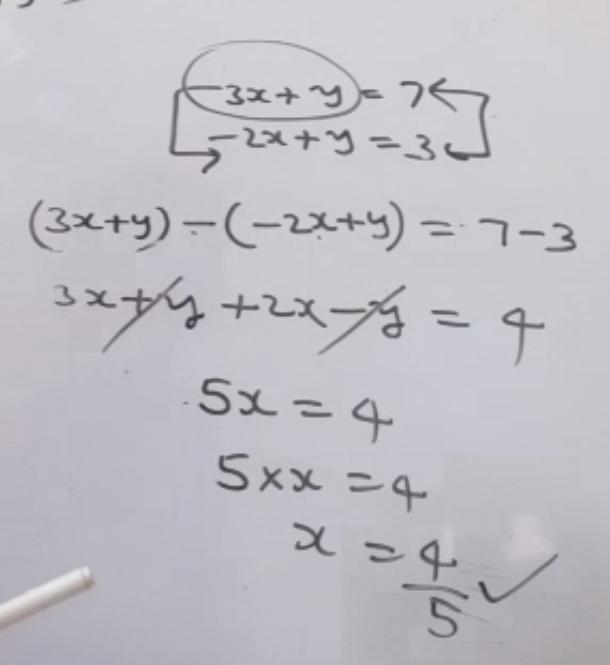

Pre - Calculus evaluate exponential derivative at a point !

Answers
Answer:
\(\displaystyle\)\(\displaystyle f'(1)=-\frac{9}{e^3}\)
Step-by-step explanation:
Use Quotient Rule to find f'(x)
\(\displaystyle f(x)=\frac{3x^2+2}{e^{3x}}\\\\f'(x)=\frac{e^{3x}(6x)-(3x^2+2)(3e^{3x})}{(e^{3x})^2}\\\\f'(x)=\frac{6xe^{3x}-(9x^2+6)(e^{3x})}{e^{6x}}\\\\f'(x)=\frac{6x-(9x^2+6)}{e^{3x}}\\\\f'(x)=\frac{-9x^2+6x-6}{e^{3x}}\)
Find f'(1) using f'(x)
\(\displaystyle f'(1)=\frac{-9(1)^2+6(1)-6}{e^{3(1)}}\\\\f'(1)=\frac{-9+6-6}{e^3}\\\\f'(1)=\frac{-9}{e^3}\)
Answer:
\(f'(1)=-\dfrac{9}{e^{3}}\)
Step-by-step explanation:
Given rational function:
\(f(x)=\dfrac{3x^2+2}{e^{3x}}\)
To find the value of f'(1), we first need to differentiate the rational function to find f'(x). To do this, we can use the quotient rule.
\(\boxed{\begin{minipage}{5.5 cm}\underline{Quotient Rule for Differentiation}\\\\If $f(x)=\dfrac{g(x)}{h(x)}$ then:\\\\\\$f'(x)=\dfrac{h(x) g'(x)-g(x)h'(x)}{(h(x))^2}$\\\end{minipage}}\)
\(\textsf{Let}\;g(x)=3x^2+2 \implies g'(x)=6x\)
\(\textsf{Let}\;h(x)=e^{3x} \implies h'(x)=3e^{3x}\)
Therefore:
\(f'(x)=\dfrac{e^{3x} \cdot 6x -(3x^2+2) \cdot 3e^{3x}}{\left(e^{3x}\right)^2}\)
\(f'(x)=\dfrac{6x -(3x^2+2) \cdot 3}{e^{3x}}\)
\(f'(x)=\dfrac{6x -9x^2-6}{e^{3x}}\)
To find f'(1), substitute x = 1 into f'(x):
\(f'(1)=\dfrac{6(1) -9(1)^2-6}{e^{3(1)}}\)
\(f'(1)=\dfrac{6 -9-6}{e^{3}}\)
\(f'(1)=-\dfrac{9}{e^{3}}\)
solve x+5y=11 and -x+4y=7 using elimination
Answers
Answer: (1, 2)
Concept:
There are three general ways to solve systems of equations:
EliminationSubstitutionGraphingSince the question has specific requirements, we are going to use elimination
Solve:
Given expressions
x + 5y = 11
-x + 4y = 7
Add both equations together to elimination [x] variable
(x + 5y) + (-x + 4y) = 11 + 7
x - x + 5y + 4y = 18
9y = 18
Divide 9 on both sides
9y / 9 = 18 / 9
\(\boxed{y=2}\)
Find the x value
x + 5y = 11 ⇔ Given equation
x + 5(2) = 11 ⇔ Substitute values of y
x + 10 = 11 ⇔ Simplify by multiplication
x + 10 - 10 = 11 - 10 ⇔ Subtract 10 on both sides
\(\boxed{x=1}\)
Hope this helps!! :)
Please let me know if you have any questions
Answer:
Stack the two equations and add them together as if they were multi-digit numbers. That will eliminate the x and then you can solve for the y. Knowing y you can then go back and solve for x.
Step-by-step explanation:
x + 5y = 11
-x + 4y = 7
---------------- "Add" the equations above to get the equation below.
9y = 18
Now you can divide both sides by 9 to see that y is equal to 2.
Now that you know that y = 2 you can substitute y in either of the two original equations. I'll use the first.
x + 5(2)= 11
x + 10 = 11
x = 1
Why is 1 neither prime nor a composite number?
Answers
Answer:
1 is neither prime nor a composite number because it only has 1 divisor, 1 and 1, and it doesn't have more than 2 integral divisors, like stated, it only has 1. So it falls in neither category.
Answer:
because
Step-by-step explanation:
A prime number has exactly two integral divisors: 1 and itself. Because it contains only one divisor, the number 1 is not a prime. A whole number with more than two integral divisors is called a composite number. So, with the exception of 0 and 1, all whole integers are either prime or composite.
.I want a way to solve the question

Answers
Answer:
2/10
Step-by-step explanation:
To do this, add all of the numbers in the bag up.
2 + 3 + 5 = 10. There are 2 yellow balls in 10. SO the answer is D.
Hope this helped and pls mark me brainliest
Answer: (D)
Step-by-step explanation: the bag contains 10 ball 5 + 3 is 8 + 2 = 10 there are only 2 balls that are blue so the answer would 2/10
Find the solution of this system of equations. Separate the x- and y- with commas.
x = -6 + y
and
-7x + 9y = 8
Answers
Answer:
x = -23
y = -17
Step-by-step explanation:
\(x = - 6 + y \\ - 7x + 9y = 8 \\ \\ - 7( - 6 + y) + 9y = 8 \\ 42 - 7y + 9y = 8 \\ 2y = 8 - 42 \\ y = \frac{ - 34}{2} \\ y = - 17 \\ \\ x = - 6 + y \\ x = - 6 + ( - 17) \\ x = - 6 - 17 \\ x = - 23\)
Answer:
Step-by-step explanation:
-7(-6 + y) + 9y = 8
42 - 7y + 9y = 8
2y + 42 = 8
2y = -34
y = -17
x = -6 - 17
x = -23
(-23, -17)
Solve by using elimination. Express your answer as an Ordered pair (-x +2y=3 3x-2y=7
Answers
Answer:
(5,4)
Step-by-step explanation:
-x+2y=3
3x-2y=7
Add the like terms( 2y and -2y)(-x and 3x)(3 and 7) together. Do this vertically. 2y and -2y cancel eachother out.
2x=10Divide both sides by 2
x=5To find y, substitute x in for y in one of the equations
-5+2y=3add 5 to both sides
2y=8Divide both sides by 2
y=4Check:
-5+2(4)=33=3Pls help step by step, loves <3 (special right triangles)

Answers
Answer:
x ≈ 30,37
y ≈ 29,00
Step-by-step explanation:
Use trigonometry:
\( \sin(38°) = \frac{9}{x} \)
Now, use the property of the proportion to find x:
\(x = \frac{9}{ \sin(38°) } ≈30.37\)
Do the same thing to find y:
\( \tan(38°) = \frac{9}{y} \)
\(y = \frac{9}{ \tan(38°) } ≈29.00\)
Enter the equation of a circle that is congruent to circle C and is centered at point P

Answers
The equation of a circle that is congruent to circle C and is centered at point P is (x - 5)² + (y - 1)² = 5².
What is the equation of a circle?In Geometry, the standard form of the equation of a circle is modeled by this mathematical equation;
(x - h)² + (y - k)² = r²
Where:
h and k represent the coordinates at the center of a circle.r represent the radius of a circle.Based on the information provided, we have the following parameters for the equation of this circle:
Center (h, k) of P = (1, 5)Radius (r) of P = 5 units.By substituting the given parameters, we have:
(x - h)² + (y - k)² = r²
(x - 5)² + (y - 1)² = 5²
Read more on equation of a circle here: brainly.com/question/15626679
#SPJ1
I need help with this stuff I don’t understand

Answers
Answer:
x = 10°
Step-by-step explanation:
By the inscribed angle theorem, the measure of an inscribed angle is half the measure of the intercepted arc.
So
x =( x + 10 )/2
2x = x + 10
2x - x = 10
x = 10°
Hope it will help :)
Which is equivalent to 3 square root 8 1/4
Answers
Answer:
8.61
Step-by-step explanation:
Calculator
for questions that require a numerical answer, you may be told to round your answer to a specified number of decimal places or you may be asked to provide an exact answer. when asked to provide an exact answer, you should enter repeating decimals in their fraction form and irrational numbers such as e^5, ln(4), or V2 in their symbolic form. consider the function f(x)= e^x +1/3x a. Find f(5), Give an exact answer b. Find f(11), Give your answer rounded to 3 decimal places
Answers
The value of f(5) is e^5 + 5/3, which is exactly 150.0798257693, and the value of f(11) is e^11 + 11/3, which is approximately 59877.808.
The function is f(x)= e^x + 1/3x
To find the value of f(5), put the value of x = 5 in the function f(x)= e^x + 1/3x. Which is equal to f(5) = e^5 + 5/3.
Similarly, to find the value of f(11), put the value of x = 11 in the function f(x)= e^x + 1/3x.
Which is equal to f(11) = e^11 + 11/3
f(11) = 59874.141715198 + 3.6666666667
f(11) = 59877.808381865
f(11) ≈ 59877.808
To know more about function, here
https://brainly.com/question/5975436
#SPJ4
help, can you tell if im right?

Answers
Answer:
Yes, all of your answers are 100% correct
Step-by-step explanation:
You correctly set the values equal to the numerator or denominator (minutes = minutes) and any value will equal the same value.
judith is planning a party for her younger brother
Answers
Answer:
COOL
Step-by-step explanation: